BZOJ5480:路径的条数

Posted on | In | | Visitors:
Words count in article: 1.8k | Reading time ≈ 9


Description

给一棵$n$个点的有标号无根树，你需要找到满足条件的路径$u−v$的条数。
我们称路径$u-v$满足条件当且仅当$u\not=v$且路径$u-v$上不存在点对
$(a,b)$,$a,b$满足$gcd(a,b)=a$。
注意：路径$u−v$和$v−u$是同一条路径。

Input

第一行一个整数$n\le10^5$
接下来$n−1$行，每行两个用空格隔开的整数$a,b$，表示边$(a,b)$

Output

一行一个整数，代表要求的答案。

Sample Input

4
3 1
3 2
3 4

Sample Output

2
//只有路径$2 − 3$和$3 − 4$满足条件

Solution

这个题的转换很有意思
我们考虑用总路径数-不合法的路径数来得到合法的路径数
那么现在问题就在于，如何求不合法的路径数
首先根据题意，枚举起点$u$，可以通过枚举$u$的倍数来得到一些不合法的路径，我们可以称之为“限制”，很容易得出：每一个不合法的路径必定至少包含一个“限制”
知道这个有什么用呢？
重头戏来了：
设$dfn[x]$为$x$点的dfs序，$cover[x]$为$x$子树中最大的dfs序
考虑不合法路径$a-b$，假设$a-b$包含路径$u-v$且$dfn[u]<dfn[v]$，$dfn[a]<dfn[b]$
分两种情况讨论：

  1. $u$是$v$的一个祖先
  2. $u$不是$v$的祖先

对于第一种情况

这时候$a,b$和$u,v$有怎样的关系呢？我们来看下面这张图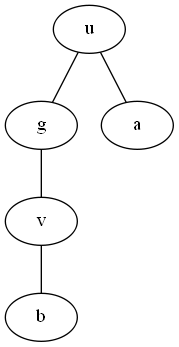
1

这时我们发现，$a$可以是$g$子树外的任意一点，$b$可以是$v$子树内的任意一点，他们对应的dfs序关系为
$dfn[a]$ $<$ $dfn[g]\;\;and\;\;dfn[v]\le dfn[b] \le cover[v]$
当然你可能会问：那如果我们先遍历图中$g$的那棵子树，上面这个关系就不成立了！（注意我们的前提条件，$a$的dfs序小于$b$）
没错，所以我们还要讨论把上图中把$a,b$交换的情况，此时关系为
$dfn[v]\le dfn[a] \le cover[v]\;\;and\;\;dfn[b] > cover[g]$

对于第二种情况

这种情况相对较简单，还是先上图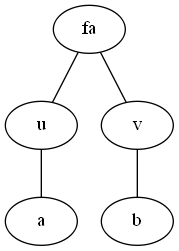
2
此时$a$是$u$子树中的任意一点，$b$是$v$子树中的任意一点
所以对应的关系就是
$dfn[u]\le dfn[a] \le cover[u]\;\;and\;\;dfn[v]\le dfn[b]\le cover[v]$

说了这么多，这有什么用啊？

考虑这样一个坐标系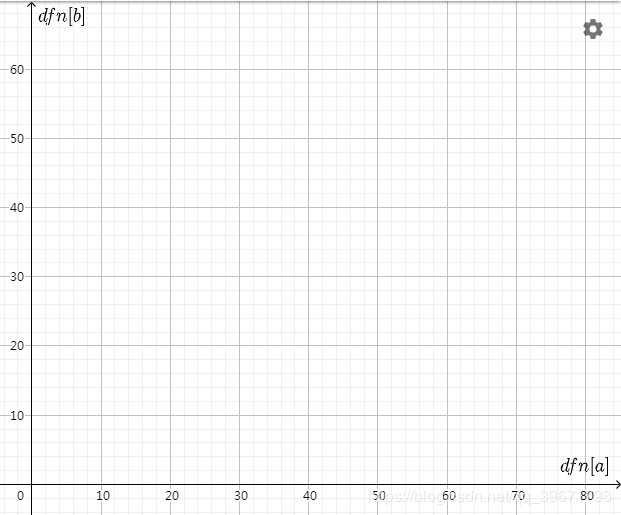3
这个坐标系的横轴是$dfn[a]$，纵轴是$dfn[b]$
再看看上面我们列出的条件，$dfn[a]$对应一个横轴上的区间，$dfn[b]$对应一个纵轴上的区间
这不是矩形嘛！
大致乱画一下，其实一堆条件（关系）就成了下面这个东西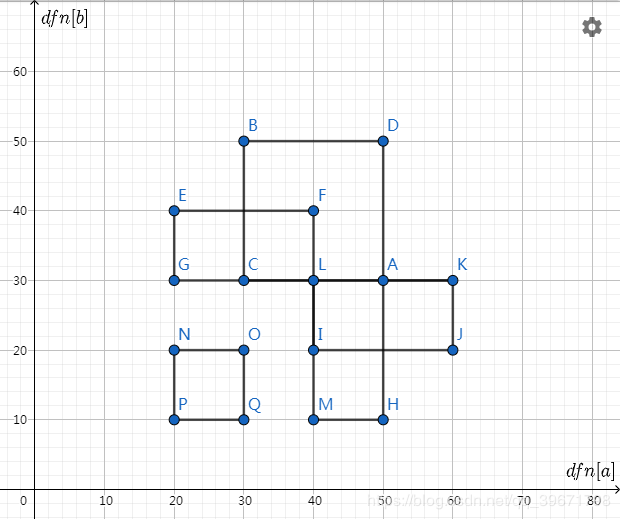
4
这些矩形内的每一个整点$(dfn[a],dfn[b])$，都是满足我们要求的东西，也就是不合法
而每一个dfs序对应唯一节点，这样我们计算这些矩形内的整点个数就能得到不合法的路径数
如何计算？线段树维护扫描线即可，只不过把求面积改成求矩形内点的个数，如果具体不清楚可以直接看代码，代码还算是比较简明的
最终统计答案，由于我们这样求出的路径是无向的，设求出的路径数为$ans$
答案就是$\dfrac{n*(n-1)}{2}-ans$

复杂度：枚举$u,v$是$O(n\ln n)$的，线段树还要再乘个$\log n$，所以总复杂度应该是$O(n\ln n\log n)$

最后献上本人丑陋的代码，现在是2019年3月28日22:06:10，目前在BZOJ是最快的代码

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
35
36
37
38
39
40
41
42
43
44
45
46
47
48
49
50
51
52
53
54
55
56
57
58
59
60
61
62
63
64
65
66
67
68
69
70
71
72
73
74
75
76
77
78
79
80
81
82
83
84
85
86
87
88
89
90
91
92
93
94
95
96
97
98
99
100
101
102
103
104
105
106
107
108
109
110
111
112
113
114
115
116
117
118
119
120
121
122
123
124
/**************************************************************
    Problem: 5480
    User: Zechariah
    Language: C++
    Result: Accepted
    Time:13152 ms
    Memory:193400 kb
****************************************************************/
 
#include <bits/stdc++.h>
#define lowbit(x) (x & -x)
#define jh(x, y) x ^= y ^=x ^= y
#define loc(x, y) (x - 1) * m + y
#define rg register
#define inl inline
#define PI 3.141592654
typedef long long ll;
const int N = 8e5 + 5, mod = 998244353, INF = 0x3f3f3f3f;
using namespace std;
namespace fast_IO {
    inl ll read() {
        rg char c;
        rg ll x = 0;
        rg bool flag = false;
        while ((c = getchar()) == ' ' || c == '\n' || c == '\r');
        if (c == EOF)return c; if (c == '-')flag = true; else x = c ^ 48;
        while ((c = getchar()) != ' ' && c != '\n' && c != '\r'&&~c)
            x = (x << 1) + (x << 3) + (c ^ 48);
        if (flag)return -x; return x;
    }
    inl ll max(rg ll a, rg ll b) { if (a > b)return a; return b; }
    inl ll min(rg ll a, rg ll b) { if (a < b)return a; return b; }
    void write(rg ll x) { if (x < 0)putchar('-'), x = -x; if (x >= 10)write(x / 10); putchar(x % 10 ^ 48); }
}
int cover[N], dfn[N], nt[N], b[N], p[N], num, id, fa[N][18], deep[N], tot, n;
struct Node {
    int left, right, min;
    ll sum;
}tree[N << 2];
struct Line {
    int l, r, v, y;
    Line(rg int l = 0, rg int r = 0, rg int y = 0, rg int v = 0) :l(l), r(r), y(y), v(v) {}
    bool operator <(const rg Line &s)const { return y < s.y; }
}e[N << 2];
inl void add(rg int x, rg int y) {
    b[++num] = y, nt[num] = p[x], p[x] = num;
    b[++num] = x, nt[num] = p[y], p[y] = num;
}
inl bool is(rg int x, rg int y) { return dfn[x] <= dfn[y] && cover[x] >= cover[y]; }
void dfs(rg int x) {
    dfn[x] = ++id;
    for (rg int e= p[x]; e; e = nt[e]) {
        if (b[e] == fa[x][0])continue;
        fa[b[e]][0] = x; deep[b[e]] = deep[x] + 1; dfs(b[e]);
    }
    cover[x] = id;
}
void build(rg int x, rg int l, rg int r) {
    tree[x].left = l, tree[x].right = r;
    if (l == r)return;
    rg int mid = l + r >> 1;
    build(x << 1, l, mid); build(x << 1 | 1, mid + 1, r);
}
inl void pushup(rg int x) {
    if (tree[x].min)tree[x].sum = tree[x].right - tree[x].left + 1;
    else tree[x].sum = tree[x << 1].sum + tree[x << 1 | 1].sum;
}
void update(rg int x, rg int l, rg int r, rg ll data) {
    if (tree[x].left == l && tree[x].right == r) {
        tree[x].min += data;
        pushup(x);
        return;
    }
    rg int mid = tree[x].left + tree[x].right >> 1;
    if (r <= mid)update(x << 1, l, r, data);
    else if (l > mid)update(x << 1 | 1, l, r, data);
    else {
        update(x << 1, l, mid, data);
        update(x << 1 | 1, mid + 1, r, data);
    }
    pushup(x);
}
inl ll query() {
    sort(e + 1, e + tot + 1);
    rg ll ans = 0;
    for (rg int i = 1; i < tot; ++i) {
        update(1, e[i].l, e[i].r, e[i].v);
        ans += tree[1].sum * (e[i + 1].y - e[i].y);
    }
    return ans;
}
inl int getfa(rg int x, rg int d) {
    for (rg int j = 17; ~j; --j)
        if (d & (1 << j))
            x = fa[x][j];
    return x;
}
inl void addedge(rg int x1, rg int x2, rg int y1, rg int y2) {
    if (1 <= x1 && x1 <= x2 && x2 <= n && 1 <= y1 && y1 <= y2 && y2 <= n)
        e[++tot] = Line(x1, x2, y1, 1), e[++tot] = Line(x1, x2, y2 + 1, -1);
}
 
int main(void) {
    n = fast_IO::read();
    for (rg int i = 1; i != n; ++i)add(fast_IO::read(), fast_IO::read());
    dfs(1); build(1, 1, n);
    for (rg int j = 1; j != 18; ++j)
        for (rg int i = 1; i <= n; ++i)
            fa[i][j] = fa[fa[i][j - 1]][j - 1];
    for (rg int i = 1; i <= n; ++i) {
        for (rg int j = i << 1; j <= n; j += i) {
            rg int x = i, y = j;
            if (dfn[x] > dfn[y])jh(x, y);
            if (is(x, y)) {
                rg int node = getfa(y, deep[y] - deep[x] - 1);
                addedge(1, dfn[node] - 1, dfn[y], cover[y]);
                addedge(dfn[y], cover[y], cover[node] + 1, n);
            }
            else addedge(dfn[x], cover[x], dfn[y], cover[y]);
        }
    }
    fast_IO::write((ll)n * (n - 1) / 2 - query());
    return 0;
}