数据结构（一）

Posted on | In | 0 | Visitors:
Words count in article: 2.5k | Reading time ≈ 10

002 _1_.jpg

基本数据结构

栈

栈是一种遵循先进后出原则的数据结构，数据在同一端入栈和出栈。

手动实现如下：

1
2
3
4
5
6
7
8
9
int stk[100005], top;//stk用于存放栈内的数据，top为栈顶，入栈和出栈都是在栈顶进行操作
void ins(int x) {
    stk[++top] = x;
    //新加入一个元素x
}
int del() {
    return stk[top--];
    //返回并删除一个元素， 出栈
}

是不是很简单呢？

C++的STL提供了stack给我们直接使用，它支持如下基本操作：

1
2
3
4
5
6
stack<dataType>name;//创建一个元素类型为dataType的栈name
name.top();//返回顶部元素的引用
name.push(x);//将x压入栈中
name.pop();//弹出栈顶元素
name.size();//返回栈中的元素个数
name.empty();//栈为空时返回true

单调栈

在栈的基础上，我们规定元素出栈的顺序必须是单调不降或单调不增的，对栈内元素的顺序没有要求。
对于单调不降的单调栈，入栈前把比要入栈的元素小的元素全部出栈。
对于单调不增的单调栈，入栈前把比要入栈的元素大的元素全部出栈。

1
2
3
4
5
6
7
8
void ins(int x) {
    //此处以单调不降的单调栈为例
    while (top && stk[top] < x) {
        fun(stk[top--]);//出栈的元素可能要进行一些操作
        //top--出栈
    }
    stk[++top] = x;
}

队列

队列是一种遵循先进先出原则的数据结构，数据在一端入队，在另一端出队。

手动实现如下

1
2
3
4
5
6
7
8
9
int q[100005], head = 1, tail;
void ins(int x) {
    q[++tail] = x;
    //从尾部入队
}
int del() {
    return q[head++];
    //从头部出队
}

C++的STL中同样提供了queue供我们使用，它支持如下基本操作：

1
2
3
4
5
6
7
queue<dataType>name;//创建一个元素类型为dataType的队列name
name.front();//返回队列中第一个元素的引用
name.back();//返回队列中最后一个元素的引用
name.push(x);//x从队列尾部入队
name.pop();//删除队列的尾部
name.size();//返回队列中元素的个数
name.empty();//队列为空时返回true

单调队列

与单调栈不同，单调队列要求队内的元素要是单调不降或单调不增的，且队首队尾都可以进行出队操作，只有队尾可以进行入队操作。
一般来说，单调队列会有一个限制的大小m，即最多只能有m个元素。
单调队列主要用于维护不同段区间内的最值，每次元素要入队时，与单调栈类似地，要让一些元素出队。

1
2
3
4
5
6
void ins(int x) {
    //以单调不降的单调队列为例
    while (head <= tail && q[tail] <= x)--tail;//删除比x小的元素
    q[++tail] = x;//x入队
    while (tail - head >= m)++head;
}

链表

先鸽着

简单数据结构

ST表

ST表用于求静态区间最值，构建复杂度$O(n\log n)$，查询复杂度只有$O(1)$!
那么ST表是怎么实现的呢？显然区间[L,R]的最值可以拆成[L,L+x]与[R-x+1,R]的最值取最值，只要L+x>=R-x+1即可。
那么我们考虑求对于区间内每个位置i，从i开始往后$2^k$个元素中的最值ST[i][k]，于是构建ST表的算法就出来了。

1
2
3
4
5
6
//以求最大值为例
//注意，这里ST[i][0]为位置i上本来的这个数
for (int j = 1; j <= log2(n) + 1; ++j)
    for (int i = 1; i + (1 << j - 1) <= n; ++i)
        ST[i][j] = max(ST[i][j - 1], ST[i + (1 << j - 1)][j - 1]);
//显然是两段的最值中取最值

查询也好说：

1
2
3
4
int query(int l, int r) {
    int k = log2(r - l + 1);
    return max(ST[l][k], ST[r - (1 << k) + 1][k]);
}

并查集

并查集用于维护集合的关系。
普通的并查集操作非常简单，直接上代码。

1
2
3
4
5
6
7
8
9
//用fa[x]表示x所在的集合
//fa[x]初始化为x本身
int findf(int x) {
    if (x == fa[x])return x;//fa[x] == x说明当前的x已经表示了一个最大的集合
    return fa[x] = findf(fa[x]);//如果fa[x] != x说明当前的集合被包含在另一个集合里
}
//如此就能找到x所在的集合

fa[findf(x)] = findf(y);//将x所在的集合合并到y所在的集合

不难看出，findf最多递归小常数次，因此并查集的复杂度是非常小的。

带权并查集（扩展并查集）

带权并查集即结点有权值的并查集，如果我们要维护元素之间可量化的属性，而且这种属性关系可以合并时，可以采用带权并查集。
带权并查集中每个元素的权值通常描述其与祖先的关系。

探究结点与祖先的关系我们可以利用向量偏移。

例题

题面

首先我们确定属性，设sum[x]为从x到x的祖先的区间和
祭出好图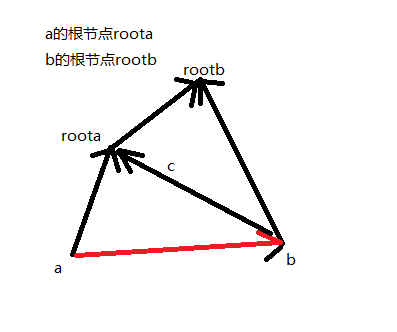
image.png

显然当roota!=rootb时，我们想要将roota和rootb合并，那么roota->rootb即sum[roota]是要更新的，可如何更新呢？
根据向量运算我们知道，(roota,rootb)=(b,rootb)-(b,roota)=(b,rootb)-(a,roota)+(a,b)
由此可得sum[roota]=sum[b]-sum[a]+w(a,b)

而当roota=rootb时，说明此时的区间通过前面的答案已经可以推出，只需要验证是否为真即可。
显然此时(a,b)=(a,root)-(b,root)
即s(a,b)=sum[a]-sum[b]

在找祖先的过程中，我们也需要对sum进行更新。
另外，我们推出的表达式是sum[r]-sum[l]的形式，因此左端点还要-1。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
int fa[N], sum[N];
int findf(int x) {
    if (x == fa[x])return x;
    int y = fa[x];
    fa[x] = findf(fa[x]);
    sum[x] += sum[y];
    return fa[x];
}

int main() {
    int n, m;
    while (~scanf("%d%d", &n, &m)) {
        for (int i = 0; i <= n; ++i)fa[i] = i, sum[i] = 0;
        int ans = 0;
        while (m--) {
            int l = fast_IO::read() - 1, r = fast_IO::read(), s = fast_IO::read();
            int rtl = findf(l), rtr = findf(r);
            if (rtl == rtr) {
                if (sum[l] - sum[r] != s)
                    ++ans;
            }
            else {
                fa[rtl] = rtr;
                sum[rtl] = -sum[l] + sum[r] + s;
            }
        }
        fast_IO::write(ans); putchar('\n');
    }
    return 0;
}

可持久化并查集

咕咕咕

优先队列（二叉堆）

首先，优先队列并不是用队列实现的，一般我们用二叉堆来实现优先队列。
那么什么是优先队列？就是队列中的元素被赋予的优先级，当我们访问优先队列时优先访问优先级高的元素。
二叉堆，其实就是一棵二叉树，它满足父节点的优先级一定大于子节点的性质，换句话说，在二叉堆中，以任意节点x为根的子树中，x的优先级是最高的，这样的话，只要构建一个二叉堆，它的根节点就是优先级最高的点。

1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19
20
21
22
23
24
25
26
27
28
29
30
31
32
33
34
//这里我们用一种比较方便的方法表示节点的左右孩子
//x * 2表示x的左孩子，x * 2 + 1表示x的右孩子，可以证明这种表示方法是不会重复的
//这样的话x / 2就可以表示x的父节点
//f[x]表示x的优先级
void shift1(int now, int len) {
    //删除了堆顶，将一个优先级小的元素放到堆顶后，通过该操作维护堆的结构
    //从顶向下去更新
    int father = now , child = father << 1;
    while (child <= len) {
        if (child < len && f[pq[child]] < f[pq[child + 1]])++child;
        if (f[pq[child]] > f[pq[father]])swap(pq[child], pq[father]);
        father = child, child <<= 1;
    }
}
void shift2(int now) {
    //加入一个元素后，从加入的元素起向上更新，维护堆的结构
    int child = now, father = child >> 1;
    while (father) {
        if (f[pq[farther]] >= f[pq[child]])break;//此时说明已经满足了堆的性质
        //因为加入元素前堆是成立的，只有加入的元素破坏了堆的结构
        swap(pq[father], pq[child]);
        child = father, father >>= 1;
    }
}
void add(int x) {
    pq[++tot] = x;
    shift2(tot);
}
dataType del() {
    dataType x = pq[1];
    pq[1] = pq[tot--];//将优先级小的放到堆顶
    shift1(1, tot);
    return x;
}

手动实现起来相当麻烦，当然，C++的STL提供了priority_queue供我们直接使用，它支持以下基本操作：

1
2
3
4
5
6
priority<dataType>pq;
pq.top();//访问堆顶元素
pq.push(x);//将x入队
pq.pop();//将堆顶出队
pq.size();//返回优先队列的元素个数
pq.empty();//优先队列为空返回true

左偏树（可并堆）

有些时候，我们需要将堆进行合并，这时候就用到左偏树。
左偏树，左偏是啥意思？意思就是对于堆内任意一棵子树，其左子树中深度最小的叶子节点的深度要大于右子树中深度最小的叶子节点的深度，这样的话从整体上看，整棵树明显左边比较重。

具体实现：我们用并查集来维护不同的节点是否在同一个堆中，下面给出合并操作

1
2
3
4
5
6
7
8
9
10
11
12
int merge(int x, int y) {//将y堆合并到x堆上，返回合并后的根节点
    if (!x || !y)return x | y;//0当然是没有这棵树啦
    if (f(x) < f(y))swap(x, y);//f(x)表示x的优先级
    //这时候就保证了x节点的优先级比y大，即y只能往x的子树合并，合并后x为根节点
    rson[x] = merge(rson[x], y);//左偏树嘛，右子树比较轻，把y往右子树合并
    if (dep[lson[x]] > dep[rson[x]])
        swap(lson[x], rson[x]);
    //永远保证rson[x]的最小深度比lson[x]的最小深度小，保证“左偏”
    dep[x] = dep[rson[x]] + 1;//x的最小深度
    fa[lson[x]] = fa[rson[x]] = x;//x为根节点
    return x;
}

合并自然不用说，如果要删除根节点，只需要合并左右子树就行了。

来发评论吧~
Powered By Valine
v1.5.2