树状数组
树状数组用于维护前缀和,支持单点修改。
树状数组的原理并不复杂:对于1 <= i < j <= n,经过若干次i+=lowbit(i),j-=lowbit(j),所得的i’和j’中必然会有唯一一对相等,所以我们只需要在修改时不断将a[i]加到c[i’]上,查询时将所有的c[i’]加起来就行了。
下面简略地说明一下,为什么这样做是对的:
首先,lowbit(x)指的是x在二进制下最低位的1,比如lowbit(3)=1,lowbit(4)=4,lowbit(6)=2。那么为什么一定会有i’和j’相等呢?
当j的二进制位大于i时,设i二进制有k位,显然i’中会包含所有k’>k,2^k’,也就是说,只要j将除最高位外所有的位都减成0,就会与某个i’相等。
当j的二进制位等于i时,从高位往低位看,必然会有某一位k使得比k位以上i和j都是1,在第k位i是0而j是1,此时又要分两种情况:
- k位以下i全是0,那么只要j把k位一下全减掉,j’就与i相等
- k位以下i有1,那么i’必然会有k位为1,k位以下全为0的情况,此时i’与j’相等
如此,就说明i’与j’必然会相等(注意:i’包含i,j’包含j),且不难看出,按上述策略找出的i’和j’是唯一的一对。
再来张树状数组的大致图像,帮助理解c[i]。

1 |
|
另外,对a的差分数组用树状数组可以实现a数组的区间修改和单点查询,只用update(l, delta),update(r+1, -delta)就行了。
树状数组的区间修改、区间查询
树状数组也可以实现区间修改、区间查询。
考察差分数组表示前缀和,即
前面的部分非常好维护,直接维护差分数组,后面的部分需要再维护一个$x\cdot d_x$1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17void update(int x, ll data) {
int k = x;
while (x <= n) {
c[x] += data;//维护差分数组
c2[x] += data * k;//维护x*d[x]
x += lowbit(x);
}
}
ll query(int x) {
ll ans = 0;
int k = x;
while (x) {
ans += (k + 1) * c[x] - c2[x];
x -= lowbit(x);
}
return ans;
}
线段树
线段树是一种非常常用的数据结构,且变化极多,这里先说最基础的线段树。
线段树,顾名思义,将区间分成一段一段,来达到区间操作的目的,那么如何分段呢?
考虑将区间[l,r]分成两半[l,mid]、[mid+1,r],这样相当于将区间对半分,那么很显然,对每个区间都这样分段,最终的段数为$O(n\log n)$。
当我们进行区间操作时,从最大的区间开始,以此去找对应要操作的区间:
- [l,r]包含在当前区间的左区间内,就接着往左区间走
- [l,r]包含在当前区间的右区间内,就接着往右区间走
- [l,r]跨过中间的分界线,那么左边操作[l,mid],右边操作[mid+1,r]
如此反复,直到找到的区间与当前操作的区间完全相同,就进行操作。
大致图像如下
另外,如果我们的区间操作涉及对区间的修改,如加减、乘除、改值,我们可以在找到的区间上打上懒标记,这样我们不用每次往下遍历完整棵线段树,当然,在遍历过程中要注意标记的下传,如果有多个标记要注意多个标记之间的关系,如乘标记不仅改变区间上的值,还改变标记的值。
1 | struct Node { |
主席树(可持久化线段树)
典例:区间第K大
给定一个长度为n的区间,给出m次查询,每次给出l,r,k,查询[l,r]中第k大的值
发明者原话:“对于原序列的每一个前缀[1···i]建立出一棵线段树维护值域上每个数出现的次数,则其树是可减的”
这话啥意思呢?就是对于序列中每一个位置i,都建立一棵线段树,这个线段树的范围是序列的值域范围,维护的是1~i中值域中的每个数出现的次数,这样的话两棵线段树的结构是完全相同的,因此对应的位置可以相减,所以用树r减去树l-1得到线段树就是区间[l,r]对应的线段树。
但是对每个位置都建立一棵线段树,空间复杂度$O(n^2\log n)$,太高了,而我们又发现,其实相邻两颗线段树有大量相同的部分,如果我们将这些相同的部分合到一起,就可以大大降低空间的负担。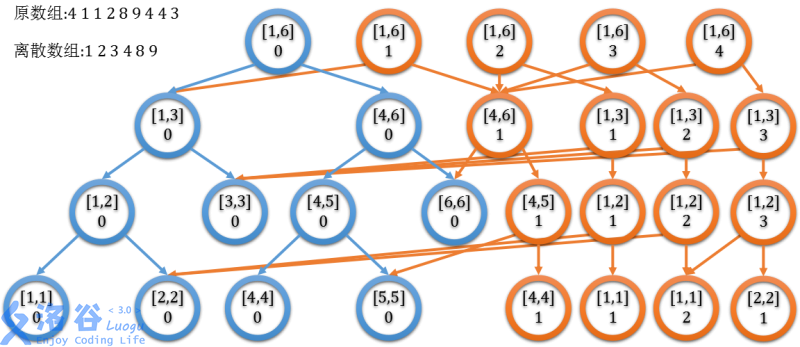
之后查询第k大就好说了,如果左区间的数字个数c>=k就往左区间找,否则在右区间找第k-c大
1 | //先建立空树 |
李超线段树
咕咕咕
扫描线
咕咕咕
树链剖分
树链剖分主要用于解决树上路径、子树相关问题。
树链剖分的思想很简单:在树上划出一些链,使得每个节点都属于且仅属于一条链,记录链的顶部,那么只需要O(1)的时间就能处理整条链的信息,从而达到缩短时间的目的。
如何划分这些链?我们采用轻重链剖分,也就是说,找到以节点x的子节点中子树大小最大的节点y(称为重儿子),将x和y划分到同一条链中。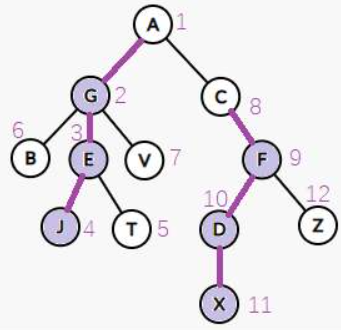
这样的话,基本就可以保证我们划分出的链尽量长,从而减少的时间更多。
树链剖分的代码实现比较麻烦,我们分步看。
首先,来看看我们需要用到什么变量和数组。1
2
3
4
5int sz[N],//子树的大小,用于求重儿子
dep[N],//节点的深度
bel[N],//节点所在链的顶部
son[N],//节点的重儿子
fa[N];//节点的父节点
我们需要求出每个点的重儿子以及深度,使用dfs。1
2
3
4
5
6
7
8
9
10
11
12
13
14//dfs1从根节点开始
void dfs1(int x) {
sz[x] = 1;//本身大小是1
for (int e = p[x]; e; e = nt[e]) {
int k = b[e];
if (k == fa[x])continue;
fa[k] = x;//k父节点是x
dep[k] = dep[x] + 1;//记录深度
dfs1(k);
if (sz[k] > sz[son[x]])son[x] = k;
//找到sz最大的子树,令其为重儿子
sz[x] += sz[k];//所有子树的大小加本身就是x子树的大小
}
}
到目前为止做的都是准备工作,接下来才是链的划分。1
2
3
4
5
6
7
8
9
10
11
12void dfs2(int x, int chain_number) {
bel[x] = chain_number;//chain_number存的就是当前链的顶部,也代表着这条链
if (son[x])//如果有子节点,将重儿子划分到同一条链中
dfs2(son[x], chain_number);
for (int e = p[x]; e; e = nt[e]) {
int k = b[e];
if (k == fa[x] || k == son[x])continue;
//son[x]已经划分了,要跳过
dfs2(k, k);
//由于我们是自顶向下dfs的,k与x又不属于同一条链,k所在的链顶部就是k本身
}
}
至此,我们就完成了树链剖分,那么如何使用呢?
比如,求LCA:1
2
3
4
5
6
7
8
9
10
11
12int LCA(int x, int y) {
//求x和y的LCA
//x和y反复往上跳,直到跳到同一条链
while (bel[x] != bel[y]) {
if (dep[bel[x]] > dep[bel[y]])swap(x, y);
//我们希望x和y都尽量往上跳,这样最节省时间,于是我们就跳链顶部的dep较小的那个
x = fa[bel[x]];//从bel[x]链跳到另一条链
}
//最终x和y在同一条链上,dep小的那一个显然就是LCA
if (dep[x] < dep[y])return x;
else return y;
}
那如果,要引入路径及子树内的修改、查询怎么办?
我们当然希望同一条链上的东西可以一起操作,这样与x和y向上跳的步骤就是一致的,那么具体怎么办呢?
考虑引入dfs序,在dfs2中,因为我们优先dfs了重儿子的分支,因此同一条链上的dfs序是连续的,同时,一棵子树内的dfs序显然也是连续的,因此我们可以在dfs序上建立线段树。1
2
3
4
5
6
7
8
9
10
11
12
13
14
15
16
17
18
19void dfs2(int x, int chain_number) {
bel[x] = chain_number;//chain_number存的就是当前链的顶部,也代表着这条链
dfn[x] = ++tot;//x的dfs序
ct[x] = dfn[x];//x子树内最大的dfs序
if (son[x]) {//如果有子节点,将重儿子划分到同一条链中
dfs2(son[x], chain_number);
ct[x] = max(ct[x], ct[son[x]]);
}
for (int e = p[x]; e; e = nt[e]) {
int k = b[e];
if (k == fa[x] || k == son[x])continue;
//son[x]已经划分了,要跳过
dfs2(k, k);
//由于我们是自顶向下dfs的,k与x又不属于同一条链,k所在的链顶部就是k本身
ct[x] = max(ct[x], ct[k]);
}
//显然,从dfn[x]到ct[x]的dfs序对应的节点与x子树内的节点一一对应
}
//其他操作都是与LCA类似的过程,对dfn[bel[x]]到dfn[x]进行操作,最后对dfn[x]到dfn[y] (dfn[x]<=dfn[y])操作
