数据结构（三）

Posted on | In | | Visitors:
Words count in article: 1.9k | Reading time ≈ 7

3e8c0627386da6c1c7a20d40d38f68bf.jpeg

平衡树

Treap（单旋）

咕咕咕

可持久化Treap

咕咕咕

Splay（双旋）

在理解splay的操作前，首先要搞清楚splay维护的是怎样的一棵树。
这棵树是一棵二叉树，它最大的特点就是，对于每个节点k，k上的权值一定大于左子树的最大权值且小于右子树的最小权值。

首先来看splay的核心操作：旋转和双旋
旋转操作，意在将节点x旋转到原本x父节点f所在的位置，那么会影响到的节点就有：x和f、x的孩子节点k1或k2、f的父亲节点gf。先看gf，gf原本的孩子节点f变成了x，只用将x放到原本f所在的位置就行；再看k1 k2，如果x是f的左孩子，那么f的权值就比x大，f应当到原本x的右孩子k2处，而k2的权值是小于f的，因此k2就到了f的左儿子处，也就是原本x所在的位置，如果x是f的右孩子则是同理；最后看x和f，颠倒父子关系即可。
于是乎，我们的旋转操作就能总结出来了：

1
2
3
4
5
6
7
8
9
10
11
12
13
14
void _rotate(int x) {//将x旋转到原本x父节点的位置
    int f = fa[x], gf = fa[f];
    c[gf][f == c[gf][1]] = x;//将x放到原本f的位置
    fa[x] = gf;
    int w = x == c[f][1];//w表示x是f的哪个孩子
    c[f][w] = c[x][w ^ 1];//原本x所在的位置变成了x相反方向的孩子
    fa[c[x][w ^ 1]] = f;
    c[x][w ^ 1] = f;//父子关系颠倒
    fa[f] = x;
    pushup(f);
    pushup(x);//这里对f和x做一些更新，因为这两个节点表示的子树发生了变化
    //当然，如果仔细想一下你会发现，在不断旋转的过程中，这个x会在下一次旋转中pushup
    //因此这里可以不写pushup(x)，而是写在splay操作完以后
}

在旋转的基础上，我们进行双旋操作。其实我们旋转的意义在于，将某个节点旋转到根节点来方便进行操作的同时，使树尽量平衡，从而降低复杂度。如果仅仅只是为了把节点放到根处操作，直接不停的旋转就行了，根本用不着splay。而我们的splay这里只有一处与直接旋转不同：如果gf、f和x成了一条直线，也就是说gf到f和f到x是同一个方向，那么我们可以先将f旋转，再将x旋转。因为这种情况下，f旋转上去时，x会被f带着向上走而不是成为gf的一个子树。通过这样的双旋操作，最终可以使得树的高度不至于太高，而是均摊$\Theta(\log n)$的水平。

1
2
3
4
5
6
7
8
9
10
11
12
void splay(int x) {
    while (fa[x]) {//fa[x]==0说明x已经到根节点了
        int f = fa[x], gf = fa[f];
        if  (gf)
            if ((f == c[gf][0]) ^ (x == c[f][0]))//gf f x不在一条线上就为1
                _rotate(x);
            else _rotate(f);//在一条线上就先转f
        _rotate(x);//再转x，一次循环的效果是将x转到了原本gf所在的位置
    }
    //pushup(x);
    rt = x;//根变成了x
}

有了这些以后，我们就可以去维护一个数集，最基本的操作就是添加、删除、查排名、查第k大数、找前驱后继等
如果这个数集是区间的下标，通过给节点附上别的权值以及标记，可以实现对区间的各种操作，尤其包括区间翻转

LCT（动态森林）

如果我们要维护一个森林，这个森林可以连边、删边，且操作后依然是森林，那么我们就可以使用LCT。
而LCT实际上是基于实链剖分，与树链剖分类似的，我们将森林里的某些路径划分为实链，每个节点属于且仅属于一条实链。
考虑到我们要动态维护森林，在这里我们使用平衡树（本人常用splay）来维护实链。
那么LCT维护的这条链是怎样的？
事实上，LCT维护的链是深度严格递增的，而splay的权值也就是深度，即每个节点x左儿子的深度比x小，右儿子的深度比x大。
明白这些以后，我们再想，如何去动态维护这些链呢？

access操作

这个操作是LCT的核心操作，其意义在于将某个点x与整棵树的根节点之间的路径划分成一条实链。
为了达到这个目的，我们需要将路径上所有连的其他边都变为虚边，再将路径上的边划分为实边即可。
下面的图片来自FlashHu的博客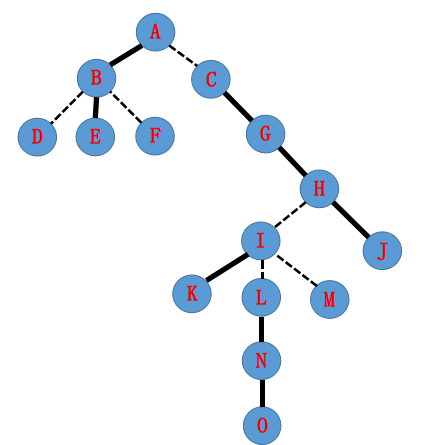
image.png

这是原始的树的图像，但显然在我们的splay里面不会是这个样子
比如说，这棵树可能实际上长这样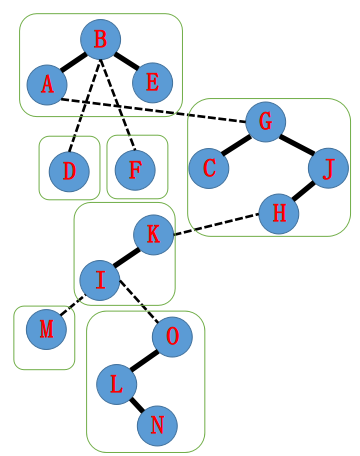
image.png

现在我们想把A与N划分成一条实链，首先当然是将N splay到当前实链的根，这样的话，断掉N-O就将深度大的节点（此处是O）全部断开，也就是变为了虚边。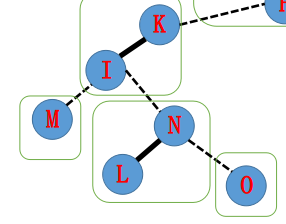
image.png

再跳到此时N的父节点I，将I与N连起来（当然是连右儿子），自然就断开了原来的右儿子，也就是“其他的边（点）”。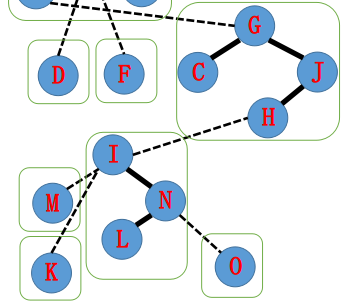
image.png

是不是找到了什么规律呢？没错，只要不断往上跳，连上右儿子并断掉左儿子，最终就能构建A-N的splay出来。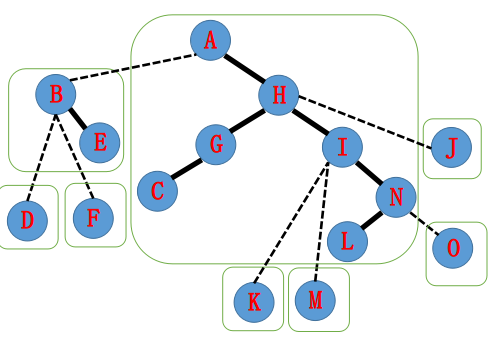
image.png

那么代码其实就很简单了

1
2
3
4
5
6
7
void access(int x) {
    for (int son = 0; x; x = fa[son = x]) {
        splay(x);
        c[x][1] = son;//连在右儿子上
        pushup(x);//对x做更新
    }
}

要特别注意的是，这里的fa维护的是原树的形状，而c维护的是splay的形状，要注意区分。

changert操作

将根节点设为x
仅仅只有access操作当然不够，如果我们想得到(x, y)的路径，我们还需要将x放到整棵树的根上，再在y处access。
其实有了access，这个操作非常简单，只需要access(x),splay(x)就行了
但这样会有一个问题，我们定义根为树中深度最小的节点，而此时的x显然是splay中深度最大的节点，所以我们需要进行区间翻转操作，这样就保证了x的深度为最小，也就是将x变为了根。

1
2
3
4
5
6
7
8
9
void pushr(int x) {
    swap(c[x][0], c[x][1]);
    r[x] ^= 1;
}//记得在splay前将所有标记下传！
void changert(int x) {
    access(x);
    splay(x);
    pushr(x);//将x所在splay翻转
}

findrt操作

查找x所在树的根节点
access(x)，然后splay(x)，接着去找深度最小的点就行了。

1
2
3
4
5
6
7
8
int findrt(int x) {
    access(x);
    splay(x);
    while (c[x][0])
        x = c[x][0];
    splay(x);//此处不影响正确性
    return x;
}

split操作

将x与y之间的路径划分到同一个splay中
前面提到过，只需要changert(x),access(y)即可

1
2
3
4
5
void split(int x, int y) {
    changert(x);
    access(y);
    splay(y);
}

link操作

将两个不在同一棵树的点连起来
显然只需要将一个点变为根，连到另一个点上即可

1
2
3
4
5
6
void link(int x, int y) {
    changert(x);
    if (findrt(y) != x)
        fa[x] = y;
    //x和y不能在同一棵树中
}

cut操作

删除x到y的边
先把x到y划到一个splay中，如果x与y相连直接删除即可

1
2
3
4
5
6
7
8
9
void cut(int x, int y) {
    changert(x);
    access(y);
    if (findrt(y) == x && fa[y] == x && !c[y][0]) {
        fa[y] = c[x][1] = 0;
        pushup(x);
    }
    //findrt(y)==x说明x与y在同一棵树中，fa[y]==x&&!c[y][0]说明x与y相连
}