图论（二）

网络流

甚么是网络流？
在有向图G=(V, E)中：

• 有唯一的一个源点S（入度为0，为出发点）
• 有唯一的一个汇点T（出毒为0，为结束点）
• 图中每条弧(u, v)都有一个非负容量c(u, v)

满足上述条件的图G称为网络流图，记为$G=(V,E,C)$

可行流

每条弧(u, v)上给定一个实数f(u, v)满足：有$0\le f(u,v)\le c(u,v)$，则f(u, v)称为弧(u, v)上的流量。
如果有一组流量满足条件：

• 源点s：流出量=整个网络流的流量
• 汇点t：流入量=整个网络流的流量
• 中间点：总流入量=总流出量

那么整个网络中的流量称为一个可行流。

最大流

在所有的可行流中，流量最大的一个流（满足流量最大的可行流可能不止一个）的流量称为最大流。

求法

最大流的求法非常多，最常用的应该是Dinic。
Dinic算法是在FF/EK算法的基础上优化的。

Ford-Fulkerson算法

在这里我们引入残余容量和增广路的概念：
残余容量是指当前的网络流图中边的容量-边的流量，增广路则是指从源点到汇点的一条所有边的残余容量都不为0的路径。
显然，直接去找增广路然后尽可能地增大流量这种做法是有问题的，比如下面这张图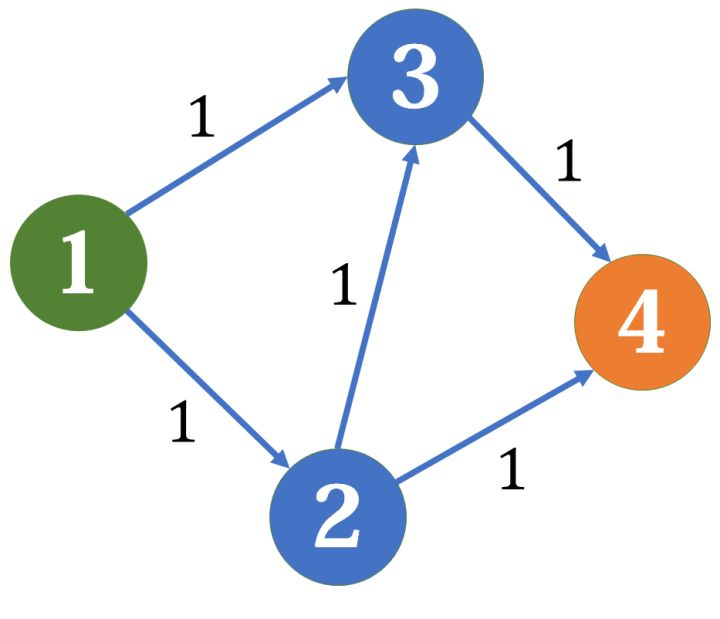

如果我们找到的增广路是1->2->3->4，最终得到的答案是1，而显然这里1->3->4和1->2->4得到的答案是2。
如何解决呢？对于每一条边我们都添上一条反向边，每当将某条边的流量增加时，增加其反向边的容量，增加的容量与增加的流量相同。
为何正确？考虑上面那张图，我们无法求出正确答案无非就是因为3->4这条边满流了，而满流的原因是1->2流过了2->3，因此如果能从1->3流到2->4，相当于中间的2->3这条边根本就没有选到，也就是说，我们撤销了2->3中的一部分流量。简要概括就是，对于一条流量本不该那么大的边，我们可以通过连到尾端的边对其进行撤销的操作。

FF算法的复杂度是$O(Mf)$，用bfs实现的FF算法即Edmond-Karp算法的复杂度是$O(nm^2)$

Dinic算法

在前面算法的基础上，就有了Dinic算法。
我们每次将网络流图进行分层，每个点只能走到比这个点高一层的点，进行dfs找增广路，重复操作直到没有增广路。
如何分层？如果一条边(u, v)的容量不为0，且v还没有被分层，那么v就是u的下一层。

模板

bool bfs() {
    memset(dist, -1, sizeof(dist));
    memset(flag, 0, sizeof(flag));
    q[++tail] = st; dist[st] = 0;
    while (head <= tail) {
        int  k = q[head++];
        for (int e = p[k]; e; e = nt[e]) {
            int kk = b[e];
            if (w[e] > 0 && dist[kk] == -1) {
                dist[kk] = dist[k] + 1;
                if (!flag[kk]) {
                    flag[kk] = true;
                    q[++tail] = kk;
                }
            }
        }
    }
    return dist[ed] > 0;
}
int dfs(int x, int minv) {
    if (x == ed)return minv;
    int flow = 0;
    for (int e = p[x], tmp; e && minv; e = nt[e]) {
        int k = b[e];
        if (dist[k] == dist[x] + 1 && w[e] > 0 && (tmp = dfs(k, min(w[e], minv - flow)))) {
            w[e] -= tmp;
            w[e ^ 1] += tmp;
            flow += tmp;
        }
    }
    if (flow < minv)dist[x] = -1;
    return flow;
}
int Dinic() {
    int ans = 0;
    while (bfs())
        ans += dfs(st, INF);
    return ans;
}

上面的代码中有几处优化：

• flow表示当前点x流出的流量，显然在x处尽量流完可以避免走重复路
• 若最终x点流出的流量比增广路（准确说应该是多路增广路）上的流量小，后面一定不可能再增广到x点了，于是将这个点的分层去掉，相当于跳过这个点

还有一种当前弧优化，即在dfs过程中记录每个点增广到哪一条边，去更新前向星建图中的$first[x]$，这样是避免重复访问不必要的边，但通常优化不是很大，也没必要用。

最小割

什么是最小割？就是一张网络流图，割掉一些边使得源点与汇点不连通，割掉的这些边的容量和的最小值。
一个著名的定理：最大流=最小割。所以求最小割我们只需要求最大流就行了。

最小割的割边

求出了最小割，我们还想知道具体是割了哪些边。
只需要从源点沿着残量网络标记下所有经过的点，标记过的点和未标记过的点之间的连边就是割掉的边。

void dfs(int x) {
    vis[x] = true;
    for (int e = p[x]; e; e = nt[e]) {
        int k = b[e];
        if (vis[k])continue;
        if (w[e])dfs(k);
    }
}
void getans() {
    dfs(st);
    for (int i = 1; i <= m; ++i)
        if (vis[edge[i].x] ^ vis[edge[i].y])
            ans[++tot] = edge[i].id;
}

最小费用最大流

最小费用最大流问题建立在最大流问题的基础之上，对每条边赋予一个单位流量的费用，问达成最大流时的最小总费用是多少。
根据我们求最大流的方法，每次我们找出一条增广路，保证这条增广路上单位流量费用的和最小，产生的贡献即为$flow\cdot fee$。
至于反向边的费用，自然是边的费用的相反数。

bool bfs() {
    memset(dist, 0x3f, sizeof(int) * (n + m + 3));
    memset(flag, 0, sizeof(bool) * (n + m + 3));
    q[0] = st, dist[st] = 0;
    int head = 0, tail = 1;
    while (head != tail) {
        int k = q[head++]; if (head == N)head = 0;
        flag[k] = false;
        for (int e = p[k]; e; e = nt[e]) {
            int kk = b[e];
            if (w[e] > 0 && dist[kk] - dist[k] > f[e]) {
                dist[kk] = dist[k] + f[e];
                pre[kk] = e;
                if (!flag[kk]) {
                    flag[kk] = true;
                    q[tail++] = kk;
                    if (tail == N)tail = 0;
                }
            }
        }
    }
    return dist[ed] != 0x3f3f3f3f;
}
int MCF() {
    int maxflow = 0, mincost = 0;
    while (bfs()) {
        int minn = INF;
        for (int i = ed; i != st; i = b[pre[i] ^ 1])minn = min(minn, w[pre[i]]);
        for (int i = ed; i != st; i = b[pre[i] ^ 1]) {
            w[pre[i]] -= minn;
            w[pre[i] ^ 1] += minn;
        }
        maxflow += minn;
        mincost += minn * dist[ed];
    }
    return mincost;
}

上下界网络流